VIDEOS

VIDEOS

VIDEOS ECUACIONES DE SEGUNDO GRADO

MARCO TEÓRICO

1.Introducción
2.Objetivos generales

2.1-Objetivos especificos

3. Importancia

4.Definicion medidadas de tendencia central

5.Clasificación
5.1.-Media Aritmética
5.2.- Mediana
5.3.- Moda

OBJETIVO GENERAL

1.-INTRODUCCION

Cuando hemos reunido un conjunto de datos, es necesario agruparlos para entender más claramente las características principales de dicho conjunto, si debemos comparar dos o más conjuntos las agrupaciones son más necesarias. Por eso es muy importante que conozcamos las diferentes medidas de tendencia central para representar adecuadamente los datos y poderlos analizar y compararlos más fácilmente.

Estas medidas de tendencia nos permiten a hacer un estudio más profundo de una determinada muestra de una población y de esta forma poder hacer un análisis más intenso y concreto para llegar a concluir sobre la muestra a estudiar.

 

2.-OBJETIVO GENERAL

Reconocer las diferentes medidas de tendencia central y su respectivo uso en la estadística en datos agrupados y datos sueltos para el estudio y calculo de una muestra teniendo en cuenta la tabla de distribución.

 

 

2.1.-OBJETIVOS ESPECIFICOS

* Examinar cada una de las definiciones estas medidas de tendencia para

* Establecer las relaciones y diferencias entre ellas.

* Explorar cada una de las ventajas y desventajas de estas medidas para posteriormente tenerlas en cuenta en la solución de problemas o situaciones de estudio

DEFINICIÓN Y CLASIFICACIÓN

3.-IMPORTANCIA

Los métodos estadísticos tradicionalmente se utilizan para propósitos descriptivos, para organizar y resumir datos numéricos. La estadística descriptiva , por ejemplo trata de la tabulación de datos, su presentación en forma gráfica o ilustrativa y el cálculo de medidas descriptivas.

Ahora bien, las técnicas estadísticas se aplican de manera amplia en mercadotecnia, contabilidad, control de calidad y en otras actividades; estudios de consumidores; análisis de resultados en deportes; administradores de instituciones; en la educación; organismos políticos; médicos; y por otras personas que intervienen en la toma de decisiones 

4.-DEFINICIÓN

 

5.-CLASIFICACIÓN

5.1.-MEDIA ARITMÉTICA O PROMEDIO 

Es aquella medida que se obtiene al dividir la suma de todos los valores de una variable por la frecuencia total. En palabras más simples, corresponde a la suma de un conjunto de datos dividida por el número total de dichos datos.

 

 

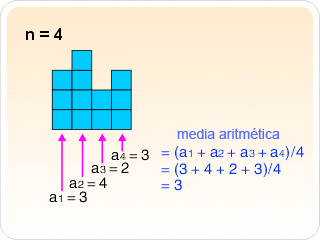
Ejemplo 1:

En matemáticas, un alumno tiene las siguientes notas:  4, 7, 7, 2, 5, 3

n = 6 (número total de datos) 

 

La media aritmética de las notas de esa asignatura es 4,8. Este número representa el promedio.

VIDEO DEMOSTRATIVO 

  

5.2.-MEDIANA

Para reconocer la mediana, es necesario tener ordenados los valores sea de mayor a menor o lo contrario. Usted divide el total de casos (N) entre dos, y el valor resultante corresponde al número del caso que representa la mediana de la distribución.

Es el valor central de un conjunto de valores ordenados en forma creciente o decreciente. Dicho en otras palabras, la Mediana corresponde al valor que deja igual número de valores antes y después de él en un conjunto de datos agrupados.

Según el número de valores que se tengan se pueden presentar dos casos:

Si el número de valores es impar, la Mediana corresponderá al valor central de dicho conjunto de datos.

Si el número de valores es par, la Mediana corresponderá al promedio de los dos valores centrales (los valores centrales se suman y se dividen por 2).

Ejemplo 1:

Se tienen los siguientes datos:  5, 4, 8, 10, 9, 1, 2

Al ordenarlos en forma creciente, es decir de menor a mayor, se tiene:  1, 2, 4,  5, 8, 9, 10

El 5 corresponde a la Md, porque es el valor central en este conjunto de datos impares.

VIDEO DEMOSTRATIVO

5.3.-MODA

La Moda es otra medida que hace referencia a la Tendencia Central que rige en una Muestra Estadística teniendo en cuenta la Posición numérica de los datos o valores que la conforman. Para obtener la Moda de una Muestra Estadística, lo único que se requiere es identificar el valor que tiene la mayor Frecuencia Absoluta

 

VIDEO DEMOSTRATIVO